关于IP包头校验和的计算

Oldtiger

[摘要]一般教科书上对IP包头校验和的计算都只有寥寥数字的陈述，没有给出一个计算过程的例子，这给学生们的学习过程带来了一定的困难。这里以《科来》捕捉到的数据包为例，说明一下计算的过程。

[关键词] 校验和计算 反码 IP包分析 科来网络分析软件

一、引子

康诰曰「克明德。」大甲曰「顾天之明命。」帝典曰「克明峻德。」皆自明也。

这是程子编的《大学》章首释“明明德”句，读完之后，什么是“明明德”、怎样才“明明德”，一头雾水，只能“皆自明也”。
对于IP包头校验和的计算，也出现“明明德”类似的情形，致我很怀疑steven、罗军舟们是不是程子门徒。请看：
steven曰：
首部检验和字段是根据IP首部计算的检验和码。它不对首部后面的数据进行计算。CMP、IGMP、UDP和TCP在它们各自的首部中均含有同时覆盖首部和数据检验和码。
为了计算一份数据报的IP检验和，首先把检验和字段置为0。然后，对首部中每个16 bit进行二进制反码求和（整个首部看成是由一串16 bit的字组成），结果存在检验和字段中。当收到一份IP数据报后，同样对首部中每个16 bit进行二进制反码的求和。由于接收方在计算过程中包含了发送方存在首部中的检验和，因此，如果首部在传输过程中没有发生任何差错，那么接收方计算的结果应该为全1。如果结果不是全1（即检验和错误），那么IP就丢弃收到的数据报。但是不生成差错报文，由上层去发现丢失的数据报并进行重传。
罗军舟曰：
头校验和字段是为了保证IP数据包头部的完整性。其计算方法是：计算之前先将头校验和字段设为0，然后将IP头部分为多个16位字(网络序)。然后对这些16位字进行二进制反码求和。计算结果存在头校验和字段。接收到一个IP数据包时，要重新计算头部校验和，并与收到数据包的头部校验和进行比较。如果两个校验和不相同则表示传输中出现了错误，lP协议就丢弃该数据包。需要说明的是，IP协议仅计算IP包头的校验和，而不计算数据区的校验和。这样做是为了减少路由器的计算量，同时也让上层协议可以为数据提供自己的校验和计算方法。
steven只有那么几个字的介绍，罗军舟也就只有这么几个字的介绍；steven没有举例子，罗军舟也就没有举例子。IP包头校验和应该怎样算？要注意哪些问题？“皆自明也”罢，哈哈。
可惜我的学生无法“皆自明”，他们坐在电脑前面两节课都还不知道如何下手计算。无奈，我只好把IP头部校验和计算分列为只有固定包头的校验和计算、IP选项长为32位整倍数的包头校验和计算和IP选项长不为32位整倍数的包头校验和计算三种情形分别说明如下。

二、只有固定包头的校验和计算
正常的IP包都不带IP选项，只有20个字节的“固定包头”(位于数据包的第0x000E~0x0021字节)。这种IP包的标志，就是第0x000E字节的值为0x45。对于这种IP包，只要把这20个字节按每2个字节一组，分别求反码相加即可。如果遇到最高位有进位，则丢弃该进位。此外，计算之前应把第0x0018、0x0019两个字节置零。
例如，下图为捕捉到的一个正常的IP包，蓝色标出的20个字节就是IP包的包头，其中蓝色标出的第一个字节(即数据包的第0x000E字节)的值为0x45，印证了它是一个正常的IP包。

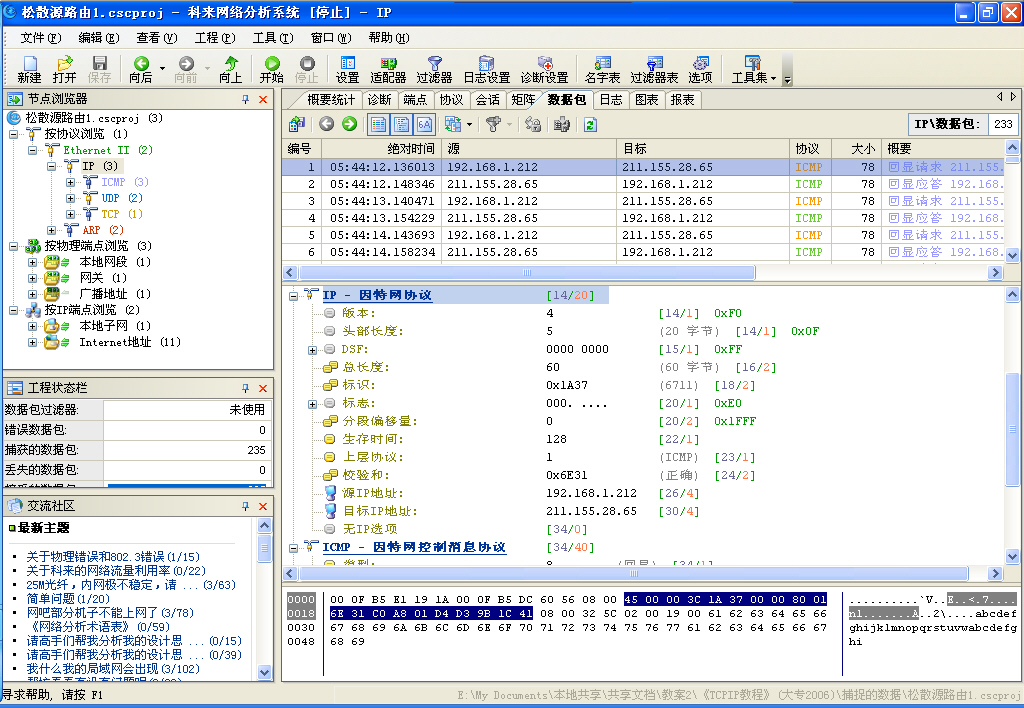
下表表示对上图的数据包IP包头进行校验和计算的过程，其中第一列是包头20个字节的编号，每两个字节作一组(将IP头部分为多个16位字)，第二列是这20个字节的十六进制值，直接取自上图蓝色标出的部分，第三列是将第二列的十六进制值转换成的二进制值，也称“原码”，第四列是对第三列取的反码，第五列则比较玄，有点像财务的三栏式记帐，它是把上一行的值与本行第四列反码的值相加得到的结果。

字节编号	十六进制值	二进制值	反码	和	备注
0x000E~0x000F	0x45 0x00	0100 0101 0000 0000	1011 1010 1111 1111
0x0010~0x0011	0x00 0x3C	0000 0000 0011 1100	1111 1111 1100 0011	1011 1010 1100 0010
0x0012~0x0013	0x1A 0x37	0001 1010 0011 0111	1110 0101 1100 1000	1010 0000 1000 1010
0x0014~0x0015	0x00 0x00	0000 0000 0000 0000	1111 1111 1111 1111	1010 0000 1000 1001
0x0016~0x0017	0x80 0x01	1000 0000 0000 0001	0111 1111 1111 1110	0100 000 1000 0111
0x0018~0x0019	0x00 0x00	0000 0000 0000 0000	1111 1111 1111 1111	0010 0000 1000 0110	预设0
0x001A~0x001B	0xC0 0xA8	1100 0000 1010 1000	0011 1111 0101 0111	0101 1111 1101 1101
0x001C~0x001D	0x01 0xD4	0000 0001 1101 0100	1111 1110 0010 1011	0101 1110 0000 1000
0x001E~0x001F	0xD3 0x9B	1101 0011 1001 1000	0010 1100 0110 0111	1000 1010 0110 1111
0x0020~0x0021	0x1C 0x41	0001 1100 0100 0001	1110 0011 1011 1110	0110 1110 0010 1101	0x6E2D

与上图第0x0018、0x0019字节相比较，很奇怪！我怎么算出来是0x6E2D而图中的是0x6E31呢？是不是我的加法有错了？我还未复查过，有空的帮我复核一下！

三、IP选项长为32位整倍数的包头校验和计算
带有IP选项的IP数据包包头长超过固定包头的20字节，其总长度由第0x000E低4位来指定。注意这低4位的值是指32位组的个数，也就是要乘上4才是字节数。对于时间戳这类的IP选项，其选项长度正好为32位的整倍数，因此包头总长直接用第0x000E低4位来乘上4就是字节数。计算校验码时，要把这总长的字节按两个一组进行反码求和。
例如，下图是一个时间戳选项的数据包：

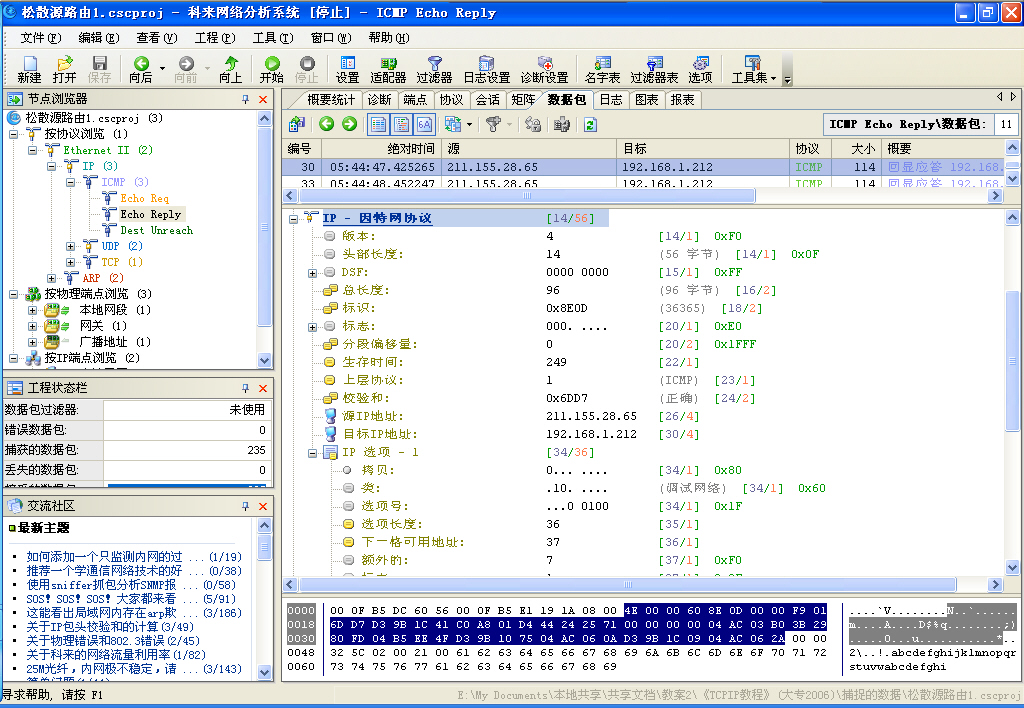
首先确定包头的位置：图中第0x000E字节值为0x4E，其低4位为0x0E，所以包头长为0x0E*4=0x38字节，即从第0x000E字节开始到第0x0045字节(图中涂蓝的部分)
分组计算：同上面的办法一样，两个字节一组，反码求和。由于包头长了，分组数也就多了

字节编号	十六进制值	二进制值	二进制反码	十六进制反码	和
0x000E~0x000F	0x4E00	0100 1110 0000 0000	1011 0001 1111 1111	0xB1FF
0x0010~0x0011	0x0060	0000 0000 0110 0000	1111 1111 1001 1111	0xFF9F	0xB19E
0x0012~0x0013	0x8E0D	1000 1110 0000 1101	0111 0001 1111 0010	0x71F2	0x2390
0x0014~0x0015	0x0000	0000 0000 0000 0000	1111 1111 1111 1111	0xFFFF	0x238F
0x0016~0x0017	0xF901	1111 1001 0000 0001	0000 0110 1111 1110	0x06FE	0x2A8D
0x0018~0x0019 [预设零]	0x0000	0000 0000 0000 0000	1111 1111 1111 1111	0xFFFF	0x2A8C
0x001A~0x001B	0xD39B	1101 0011 1001 1011	0010 1100 0110 0100	0x2C64	0x56F0
0x001C~0x001D	0x1C41	0001 1100 0100 0001	1110 0011 1011 1110	0xE3BE	0x3AAE
0x001E~0x001F	0xC0A8	1100 0000 1010 1000	0011 1111 0101 0111	0x3F57	0x7A05
0x0020~0x0021	0x01D4	0000 0001 1101 0100	1111 1110 0010 1011	0xFE2B	0x7830
0x0022~0x0023	0x4424	0100 0100 0010 0100	1011 1011 1101 1011	0xBBDB	0x340B
0x0024~0x0025	0x2571	0010 0101 0111 0001	1101 1010 1000 1110	0xDA8E	0x0E99
0x0026~0x0027	0x0000	0000 0000 0000 0000	1111 1111 1111 1111	0xFFFF	0x0E98
0x0028~0x0029	0x0000	0000 0000 0000 0000	1111 1111 1111 1111	0xFFFF	0x0E97
0x002A~0x002B	0x04AC	0000 0100 1010 1100	1111 1011 0101 0011	0xFB53	0x09EA
0x002C~0x002D	0x03B0	0000 0011 1011 0000	1111 1100 0100 1111	0xFC4F	0x0639
0x002E~0x002F	0x3B29	0011 1011 0010 1001	1100 0100 1101 0110	0xC4D6	0xCB0F
0x0030~0x0031	0x80FD	1000 0000 1111 1101	0111 1111 0000 0010	0x7F02	0x4A11
0x0032~0x0033	0x04B5	0000 0100 1011 0101	1111 1011 0100 1010	0xFB4A	0x455B
0x0034~0x0035	0xEE4F	1110 1110 0100 1111	0001 0001 1011 0000	0x11B0	0x570B
0x0036~0x0037	0xD39B	1101 0011 1001 1011	0010 1100 0110 0100	0x2C64	0x836F
0x0038~0x0039	0x1075	0001 0000 0111 0101	1110 1111 1000 1010	0xEF8A	0x72F9
0x003A~0x003B	0x04AC	0000 0100 1010 1100	1111 1011 0101 0011	0xFB53	0x6E4C
0x003C~0x003D	0x060A	0000 0110 0000 1010	1111 1001 1111 0101	0xF9F5	0x6841
0x003E~0x003F	0xD39B	1101 0011 1001 1011	0010 1100 0110 0100	0x2C64	0x94A5
0x0040~0x0041	0x1C09	0001 1100 0000 1001	1110 0011 1111 0110	0xE3F6	0x789B
0x0042~0x0043	0x04AC	0000 0100 1010 1100	1111 1011 0101 0011	0xFB53	0x73EE
0x0044~0x0045	0x062A	0000 0110 0010 1010	1111 1001 1101 0101	0xF9D5	0x6DC3

四、IP选项长不为32位整倍数的包头校验和计算

[ 本帖最后由 Oldtiger 于 2006-11-7 10:06 编辑 ]

菜鸟人飞

好帖，内容严谨，质量高。
期待三、四两部份的内容。

快乐3幸福4

哇，厉害啊，看得有点晕呼呼的，回家再看一遍，。

yswnhm

站个座！！！！！！！！！！！

aishangni

非常感谢！看了2篇，还是一个字，晕

gezi1234

精彩！以前看stevens写的这段我就疑惑进位该怎么办……？现在明白了 。多谢老虎做了这么详尽的解答！

playerwhj

值得大家好好看看！！

liuxg615

i love this web,thx

wsw111

呵呵，学了不少东西，谢谢了

zhourobinson

此文作者对“1's complement sum” 理解有误，详情请参考RFC1071 Computing the Internet Checksum.

hopehands

看完了。。。看晕了哈

allen823

哎呀妈呀,好东西啊!!!

wukongszs

看来得打好基础才能看明白~~

zhongheihu

谢谢！！！辛苦了！！！